Pure Technologiesピュア・テクノロジーズ株式会社

Development開発実績

ホーム開発実績最適化計算を使った配送システムのデモ

Demonstration of delivery system最適化計算を使った配送システムのデモ

新百合ヶ丘駅北口をスタート地点として、全ての目的地(新百合ヶ丘駅周辺の学校、公共の施設、公園の計10箇所)を通る最短経路を求めるデモです。

スタート地点 小学校 大学 警察署 消防署 税務署 郵便局 公園
近日デモ公開予定

経路順序

■→■→■→ ■→■→■→ ■→■→■→ ■→■→■→ ■→■→ ･･････

最短経路を探索する方法について

全探索

全ての目的地を通る経路を全パターン算出して最短経路を求める。全パターンを計算するため、目的地が増えるほど計算量は指数的に増加する。

SA法による探索

SA法で最短経路を求める。計算量は指定された反復回数に比例する。

※SA法による探索では経路パターンをランダムで抽出するため、以下の可能性があります。

1．探索毎に探索結果が異なる。
2．(反復回数が小さい場合)最短経路もしくは近似解が求められない。

※ SA（シミュレーテッド・アニーリング）法とは？

シミュレーテッド・アニーリング（Simulated Annealing：SA）は、Kirktpatrickらによって提案された組み合わせ最適化問題を解く汎用近似解法の一つである。

ほとんどの組み合わせ問題は、問題が大きくなると組み合わせ数が指数的に増大するために真の最適解を求めるのが実質的に不可能になってしまうのに対し、SAでは局所探索をランダムに繰り返し行うことで解を求める。更に解に改良が見られない場合でも確率的に改悪方向への移動を認めるために局所解に陥りにくく、良好な近似解を求めることができる。

長所

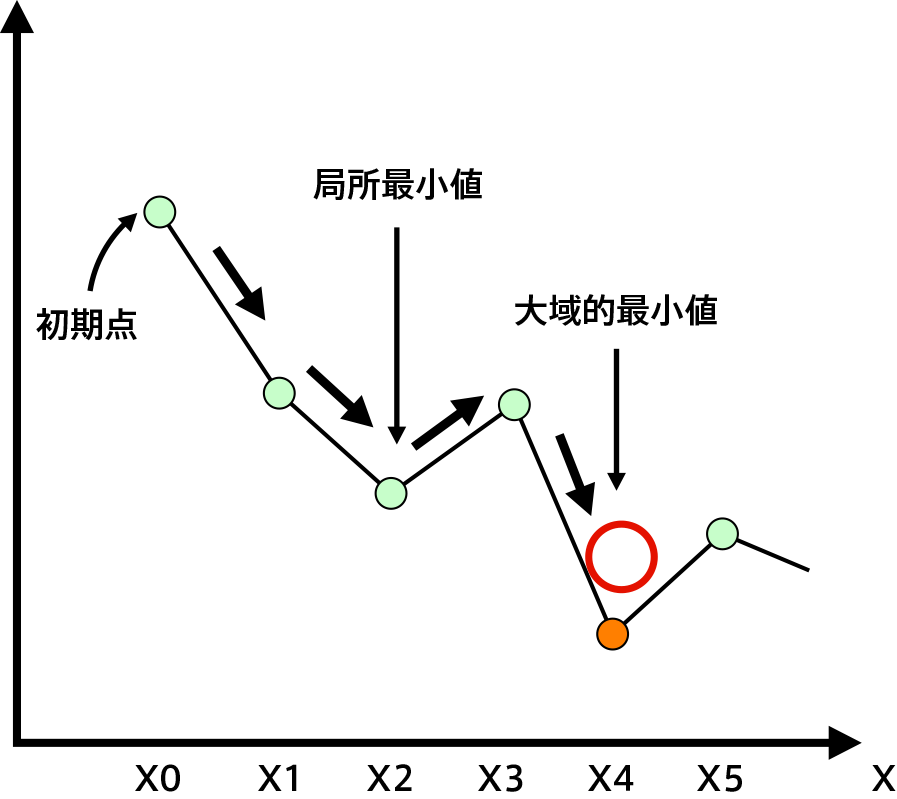
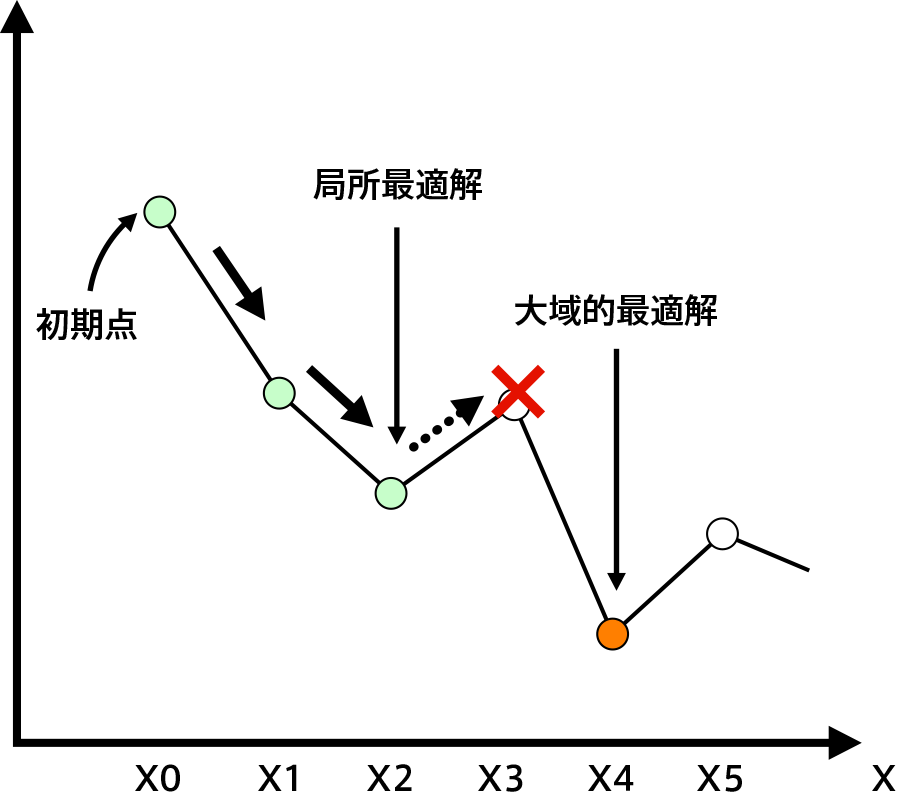
1．局所解に陥りにくい

最急降下法といった古典的な最適化解法は、初期値の与え方によって往々にして局所最適解に陥りやすい。これに対し、SAでは解の改良方向を改悪方向へも探索を進めることで真の最適解に到達することが可能である。

2．多くの問題に適用できる

アルゴリズムが汎用にできているために広範囲に渡る問題、複雑な式や確率的な式になる問題でも適用可能である

短所

1．計算量が多い

最適解を得るのに非常に多くの計算量を要する。

2．個別にパラメータを設定する必要がある

汎用解法であるために、問題を解く場合には、配送経路であれば交通量や道路の広さといったパラメータチューニングなどを個別に行う必要がある。